318. Binomial coefficients 1

Let n be a non-negative integer. Let

n! = 1 * 2 * ... * n (0! = 1),

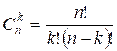
You are given the numbers n and k. Calculate .

Input. The first line contains the number of test cases t (t ≤ 50). Each of the next t lines contains two integers n and k (0 ≤ n < 2⁶⁴, 0 ≤ < 2⁶⁴).

Output. Print t lines, each contains the value for corresponding test.

Sample input

Sample output

0 0

1 0

1 1

2 0

2 1

2 2

SOLUTION

combinatorics

Algorithm analysis

Computations will be performed using 64-bit unsigned integers (unsigned long long). Its obvious that

= =

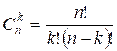Let’s assign the value of the variable res to 1. Then multiply it by for all i from 1 to k. Each time the division by i will yield an integer result, but multiplication can cause overflow. Let d = GCD(res , i). Then let’s rewrite the operation

res = res * (n – i + 1 ) / i

res = (res / d) * ((n – i + 1 ) / (i / d))

In this implementation we’ll avoid overflow (the answer is 64-bit unsigned integer). Note that first we need to perform the division (n – i + 1 ) / (i / d), and then multiply res / d by the resulting quotient.

To compute , we must run k iterations. But what to do if we want to compute ? The answer is no more than 2⁶⁴, so such input values are possible. As long as = , then for n – k < k we should assign k = n – k.

Example

Consider the next sample:

= =

Let res = 15, and we need to make a multiplication res * = 15 *. Compute d = GCD(15 , 3) = 3. So 15 * = (15 / 3) * = 5 * = 20.

Algorithm realization

The gcd function computes the greatest common divisor of a and b.

unsigned long long gcd(unsigned long long a, unsigned long long b)

{

return (!b) ? a : gcd(b,a % b);

}

The Cnk function computes the value of the binomial coefficient .

unsigned long long Cnk(unsigned long long n, unsigned long long k)

{

unsigned long long CnkRes = 1, t, i;

if (k > n - k) k = n - k;

for(i = 1; i <= k; i++)

{

t = gcd(CnkRes, i);

CnkRes = (CnkRes / t) * ((n - i + 1) / (i / t));

}

return CnkRes;

}

The main part of the program. Read the input data. Sequentially process the test cases.

scanf("%d",&t);

while(t--)

{

scanf("%llu %llu",&n,&k);

res = Cnk(n,k);

printf("%llu\n",res);

}

Java realization

Java does not have unsigned type, so we’ll use BigInteger class.

import java.util.*;

import java.math.*;

public class Main

{

static BigInteger Cnk(BigInteger n, BigInteger k)

{

BigInteger ONE = BigInteger.ONE, CnkRes = ONE;

if (k.compareTo(n.subtract(k)) > 0) k = n.subtract(k);

for(BigInteger i = ONE; i.compareTo(k) <= 0; i = i.add(ONE))

CnkRes = CnkRes.multiply(n.subtract(i).add(ONE)).divide(i);

return CnkRes;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int tests = con.nextInt();

while(tests-- > 0)

{

BigInteger n = con.nextBigInteger();

BigInteger k = con.nextBigInteger();

BigInteger res = Cnk(n,k);

System.out.println(res);

}

Python realization – comb

To compute the binomial coefficient, we shall use the built-in function

comb(n, k) =

import math

Read the number of test cases t.

t = int(input())

for _ in range(t):

Read the input data of the current test case.

n, k = map(int, input().split())

Compute and print the answer.

res = math.comb(n, k)

print(res)

Python realization

The Cnk function computes the value of the binomial coefficient .

def Cnk(n, k):

res = 1

if k > n - k: k = n – k

for i in range(1, k + 1):

res = res * (n - i + 1) // i

return res